URPM – Czy wiesz, że …
Czy wiesz, że …
W module statystycznym systemu URPM można wykonać test, aby porównać wartości zmiennej w więcej niż dwóch niezależnych grupach.
Aby wykonać test zmiennej (wyszukanej w jednym z kroków scenariusza) w co najmniej trzech grupach (określonych wartościami innej zmiennej) należy w prawym górnym rogu okna scenariusza kliknąć na przycisk „Moduł statystyczny”. Następnie należy wybrać szóstą opcję, „Porównaj wiele niezależnych grup” na liście „Testy istotności” na zakładce „Statystyki”. Pojawi się poniższe okno. W pierwszym polu „Zmienna grupująca” należy wybrać zmienną. W drugim polu „Zmienna zależna” należy wybrać testowaną zmienną z listy. Można wskazać kilka zmiennych i dla każdej z nich zostanie wykonany osobny test.
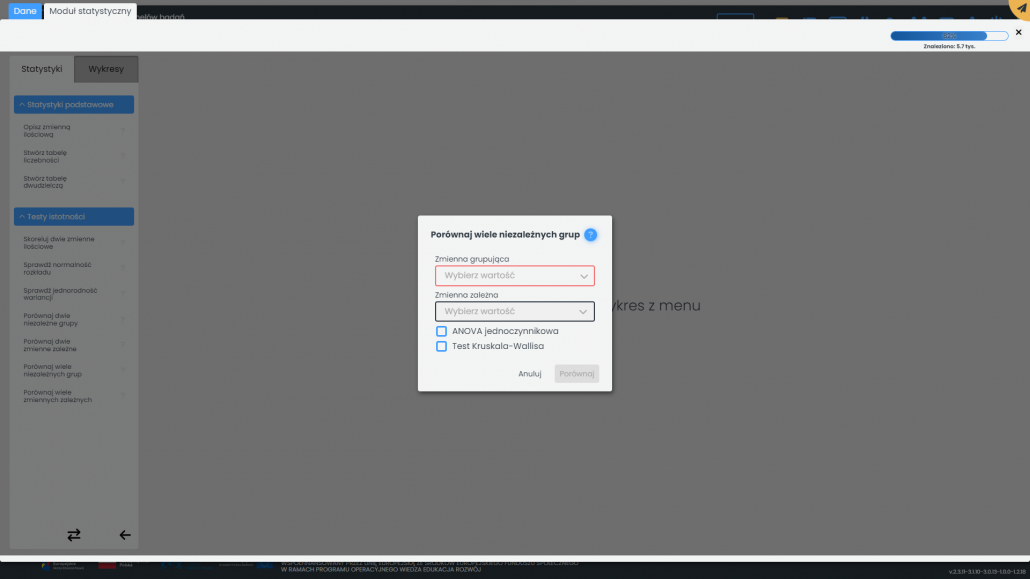
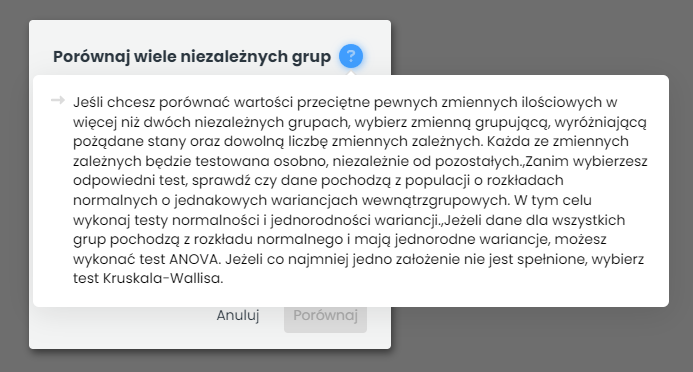
Do wyboru jest jeden z dwóch testów. Podpowiedź, który test należy wybrać można uzyskać klikając na znak zapytania przy nazwie okna.
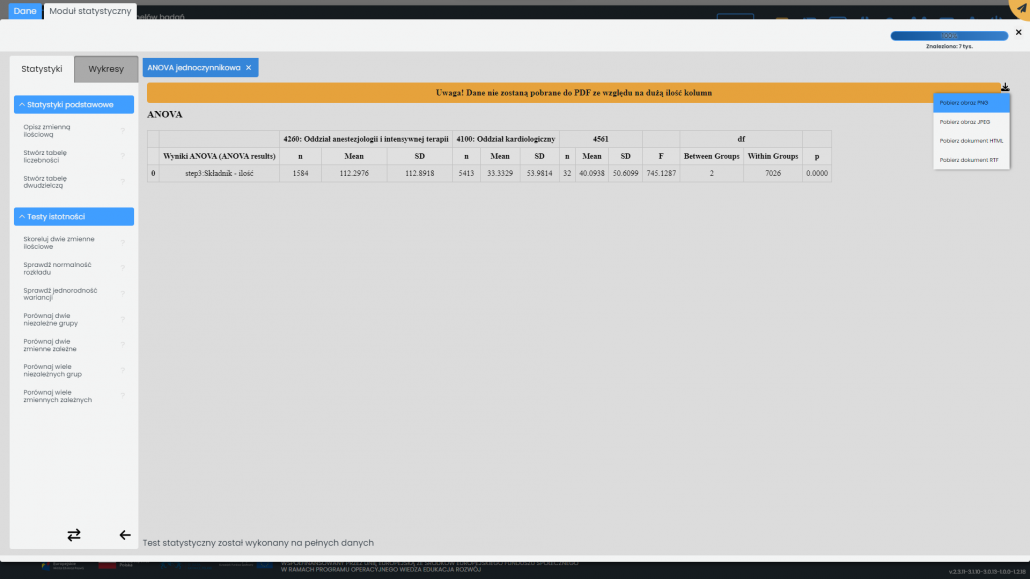
Test ANOVA należy zaznaczyć, jeśli testowana zmienna ma rozkład normalny oraz jednorodne wariancje w każdej z grup. Po kliknięciu przycisku „Porównaj” pojawi się tabela. Wyliczone wartości mają następujące znaczenie: n — liczba przypadków w grupie, Mean – średnia w grupie (ang. mean value), SD – odchylenie standardowe w grupie (ang. standard deviation), F – wartość statystyki testowej F, df – liczba stopni swobody międzygrupowych (Between Groups) i wewnątrzgrupowych (Within Groups), p – wartość p. Kliknięcie na symbolu „strzałki” z prawej strony okna rozwinie menu umożliwiające zapisanie tabeli do pliku o wskazanym formacie.
Jeżeli nie jest spełniony przynajmniej jeden warunek, to należy wykonać test Kruskala-Wallisa. W tabeli znajdują się wyliczone wartości: n – liczba przypadków w grupie, MED – mediana w grupie (ang. median), Q1 – pierwszy kwartyl (ang. lower quartile), Q3 – trzeci kwartyl (ang. upper quartile), df – liczba stopni swobody równa k-1 (gdzie k to liczba grup), Chi-square – wartość statystyki testowej Chi kwadrat, p – wartość p.

Sposób wykonania porównania zmiennej w więcej niż dwóch niezależnych grupach wyjaśniono w instrukcji
https://urpm.sum.edu.pl/dig-guide/statystyki/wiele_grup.html.




